Question

How do i figure out with points of each go with each ratio

Answer 1

Point A partitions MS in a 2:5 ratio.

Point K partitions MS in a 5:2 ratio.

Point R partitions MS in a 1:1 ratio.

Explanation:

Point P(x,y) that partitions MS is a 2:5 ratio. I am going to draw the situation here.

Applying this, we can find the x and y coordinates of P.

x-coordinate:

x-coordinate of M is 2.

x-coordinate of P is x.

x-coordinate of S is 10.

Distance of MS: 10 - 2 = 8

Distance of MP: x - 2

Since the distance of MP is 2/7 of the distance of MS.

`x-2=(2)/(7)\ast8`
`x-2=(16)/(7)`
`x=(16)/(7)+2=(16)/(7)+(14)/(7)=(30)/(7)`

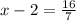
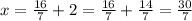
Point A has x-coordinate of 30/7. So

Point A partitions MS in a 2:5 ratio.

Now, we want to find the point that partitions the segment in a 5:2 ratio. So

We want to find point P(x,y).

Now, we have to solve:

`x-2=(5)/(7)\ast8`
`x-2=(40)/(7)`
`x=(40)/(7)+2=(40)/(7)+(14)/(7)=(54)/(7)`

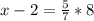
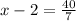
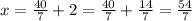
Point K has x-coordinate 54/7. So

Point K partitions MS in a 5:2 ratio.

Finding the point that partitions in a 1:1 ratio.

Point P(x,y)

Then, we have to solve the following equation:

`x-2=(1)/(2)\ast8`

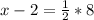
So

x - 2 = 4

x = 6

Point R has x-coordinate equals to 6. So

Point R partitions MS in a 1:1 ratio.