Question

Given the function: f(x)=√x-2 f(x) = -(x + 2) a) Write the domain and range for the function above 1 b) Describe the transformation of the function from the parent function Vertical Shift: Horizontal Shift: Reflection over X Reflection over y:

Answer 1

The function we have is:

`f(x)=\sqrt[]{-(x+2)}`

Part a.

Step 1. Find the domain.

The domain is the allowed values for the variable x.

In this case, since we have a square root, the rule is that we cannot have the total value inside the square root to be less than 0. (In the real numbers, there are no defined square roots of negative numbers).

Thus, the condition for x is:

`-(x+2)\ge0`

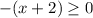
--the expression inside the square root has to be greater to or equal to 0.

From the condition, we solve for x:

`\begin{gathered} -x-2\ge0 \\ \text{add x to both sides of the equation:} \\ -2\ge x \end{gathered}`

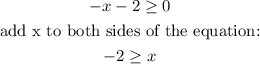
x has to be greater than or equal to -2.

The domain can be written as follows:

`x\leq-2`

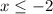
Or it can also be written in interval form:

`(-\infty,-2\rbrack`

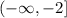
Step 2. Find the range of the function.

The range of a function is the values that the function can return as the values of f(x).

As we saw in step 1, the smaller value that the expression inside the square root can take is 0, thus, the smaller value that f(x) can take is the square root of 0, which is 0.

This tells us that the allowed values for f(x) (the range) are any values equal to or greater than 0:

`y\ge0`

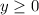
That is the range of the function. Which can also be written in interval form:

`\lbrack0,\infty)`

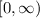
Part b.

Step 3. We need to describe the transformation from the parent function. Since the function we have is a square root of an expression that includes x, the parent function is:

`f(x)=\sqrt[]{x}`

Which looks as follows:

And to compare it with the given function, we also graph it:

The graph of

`f(x)=\sqrt[]{-(x+2)}`

is:

As you can see by comparing the parent function and our function, there were two transformations made:

A horizontal shift of -2 and a reflection across the y axis.

Part c. The graph of the function is given in step 3.