Question

Are the following lines Parallel, Perpendicular, or neither: y = -4x + 1 and 4y = x + 3

Answer 1

Given:

y = -4x + 1

4y = x + 3

Since the first equation is already in slope-intercept form, let's rewrite the second equation to slope-intercept form.

4y = x + 3

Divide through by 4:

`\begin{gathered} (4y)/(4)=(x)/(4)+(3)/(4) \\ \\ y=(1)/(4)x+(3)/(4) \end{gathered}`

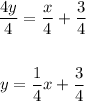
Parallel lines have similar slope, while the slope of perpendicular lines are negative reciprocals of each other.

Using:

y = mx + b

Where m = slope

Slope of the first line y = -4x + 1 is -4

Slope of the second line: = ¼

`y=(1)/(4)x+(3)/(4)`

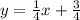
The negative reciprocal of -4 is ¼.

Therefore, the lines are perpendicular to each other since the slope of the second line is the neagtive reciprocal of the first line.

ANSWER:

Perpendicular lines