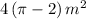1 Answer

Pontus · Answer 1 · 2023-03-08T05:45:58+0000

The formula to calculate the area of the shaded piece(A) is,

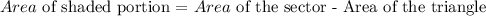
$Area\text{ of shaded portion = }Area\text{ of the sector - Area of the triangle}$

The formula for the area of the sector(A1) is,

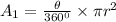
$A_1=(\theta)/(360^0)*\pi r^2$

Given

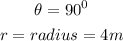
$\begin{gathered} \theta=90^0 \\ r=radius=4m \end{gathered}$

Therefore,

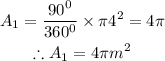
$\begin{gathered} A_1=(90^0)/(360^0)*\pi\text{\lparen4\rparen}^2=4\pi \\ \therefore A_1=4\pi m^2 \end{gathered}$

The formula for the area (A2) of the triangle is,

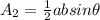
$A_2=(1)/(2)absin\theta$

Given

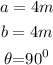
$\begin{gathered} a=4m \\ b=4m \\ \theta\text{=90}^0 \end{gathered}$

Therefore,

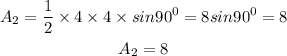
$\begin{gathered} A_2=(1)/(2)*4*4* sin90^0=8sin90^0=8 \\ A_2=8 \end{gathered}$

Therefore, the area of the shaded piece(A) is

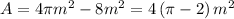
$A=4\pi m^2-8m^2=4\left(\pi-2\right)m^2$

Hence, the answer is

$4\left(\pi -2\right)m^2$

Please log in or register to add a comment.