Given:
Fundamental frequency = 262 Hz.
Temperature = 20 degrees celcius
Let's find the length of the pipe.
Apply the resonant frequency:
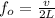
Where:
L is the length.
To find the length, rewrite the equation for L:
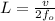
Where v is te speed, to find the speed, we have:
![\begin{gathered} v=331\sqrt[]{1+(T)/(273)} \\ \\ \text{Where:} \\ T=20^0c \\ \\ v=331\sqrt[]{1+(20)/(273)} \\ \\ v=331\sqrt[]{1+0.07326} \\ \\ v=331(1.03598) \\ \\ v=342.9\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/xiylcsz6gderpnfvqi2uluc7446tbc3nxt.png)
Thus, to find the length, we have:
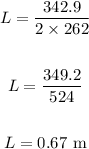
Therefore, the length of the pipe is 0.67 m.
ANSWER:
0.67 m