Question

8. Which pairs of fractions are equivalent mark all that apply. 8/12 and 2/3 4/5 and

Answer 1

We can check if two fractions are equivalent by doing cross multiplication and see if the result is true.

For example, for 8/12 and 2/3 we have the following:

`\begin{gathered} (8)/(12)=(2)/(3) \\ \Rightarrow8\cdot3=2\cdot12 \\ \Rightarrow24=24 \end{gathered}`

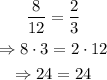
since we have that 24 = 24, this means that the fractions are equivalent.

For the next fraction, we have 3/4 and 20/28, then:

`\begin{gathered} (3)/(4)=(20)/(28) \\ \Rightarrow3\cdot28=4\cdot20 \\ \Rightarrow84=80 \end{gathered}`

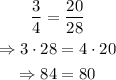
in this case we have that 84 = 80, which is never true, thus, the fractions are not equivalent.

For the remaining two cases,we have:

`\begin{gathered} (4)/(5)=(12)/(16) \\ \Rightarrow4\cdot16=5\cdot12 \\ \Rightarrow64=60 \end{gathered}`

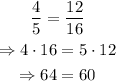
and:

`\begin{gathered} (7)/(10)=(21)/(30) \\ \Rightarrow7\cdot30=10\cdot21 \\ \Rightarrow210=210 \end{gathered}`

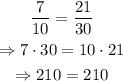
therefore, only 8/12 and 2/3,

and 7/10 and 21/30

are equivalent fractions