Let v be the number of students in each Van and b be the number of students in each Bus.
If High School A filled 9 vans and 10 buses, the toal number of students is:
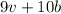
And this is equal to 653, so:
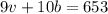
If High School B filled 9 vans and 6 buses, the toal number of students is:
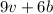
And this is equal to 417, so:
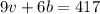
So, the system of equations is:
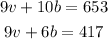
If we substract the second equation from the first, we will have:
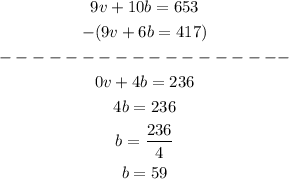
With the value for b, we can substitute into either eqution and solve for v:
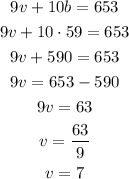
Thus, the number of students in each Van is 7 and the number of students in each Bus is 59.