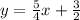Given:
The given line passes through (2,4) and (-6,-6)
Required: The equation of the line
Step-by-step explanation:
First, find the slope using the two point formula.
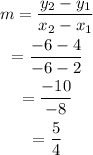
The slope-intercept form of a line is of the form y = mx+c, where m is the slope and c is the y-intercept.
Substitute the obtained value of m into y = mx+c.
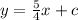
Plug the point (2, 4) into the equation to find c.
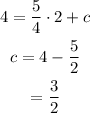
Substitute the value of c into y = (5/4)x+c.
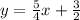
Final Answer: