Determine the equilibirium position for the weight.
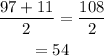
Determine the amplitude for the Simple harmonic function.
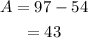
Determine the time taken by weight for the one complete cycle.
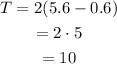
The formula for the angular frequency is,
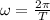
Substitute the values in the formula to determine the angular frequancy of the weight.
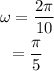
Determine the general equation of motion of weight.
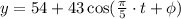
For t = 0.6 y = 11.
Determine the phase difference angle for t = 0.6 and y = 11.
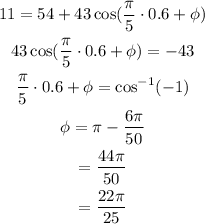
So equation for the height above the floor as a function of time is,
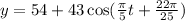
Plot the graph of the height function.
Substitute 0 for t in the equation to determine the weight height at time zero.
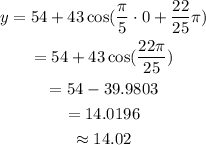
So height above the floor at time zero is 14.02 cm.