Question

Given that sinø =-1/2 and ø lies in the quadrant IV, find the following value. Tanø

Answer 1

Step-by-step explanation:

Let us sketch the angle ø.

As can be seen from the triangle above,

`\sin\phi=-(1)/(2)`

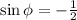
Furthermore,

`\tan\phi=-(1)/(x)`

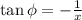
we just need to find the value of x.

To find the value of x, we use pythagoras's theorem.

`x^2+1^2=2^2`
`x^2+1=4`

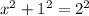
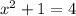
subtracting 1 from both sides gives

`x^2=4-1`
`x^2=3`

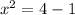
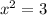
taking the sqaure root of both sides gives

`x=√(3)`

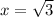
with the value of x in hand, we now have

`\tan(\phi)=-(1)/(x)=-(1)/(√(3))`
`\boxed{\tan\phi=-(1)/(√(3)).}`

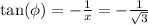
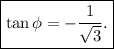
which is our answer!