Given:
19, 180, 181
To be able to determine if the given lengths form a right triangle, the following condition must be met:
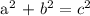
Let's check.
a.) At a = 19, b = 180, c = 181
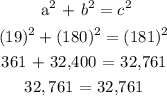
Therefore, the given lengths could form a right triangle at a = 19, b = 180 and c = 181.
The answer is yes.
It just happened to be that we got the right answer on the first try, you must also examine at a = 180, b = 181, c = 19 and a = 181, b = 19, c = 180 if the first try didn't meet the right condition.
If you failed to get, then the given lengths could not form a right triangle. The answer would be no.