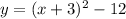Question

Instructions: Given the function in standard form, use completing the square to write the function in vertex form and then identify the vertex.

Answer 1

Given the function in standard form:

`y=x^2+6x-3`

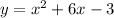
• First, we need to find the vertex, V = (h, k), as follows:

`h=(-b)/(2a)`

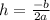
where a = 1, b = 6, and c = -3; then:

`h=(-6)/(2)=-3`
`\begin{gathered} k=f(-3) \\ k=(-3)^2+6(-3)-3 \\ k=-12 \end{gathered}`

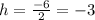
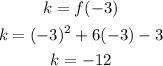
The vertex of the quadratic function is V = (-3, -12).

• Vertex form of the quadratic function:

`y=a\left(x-h\right)^2+k`

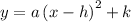
Replacing in the equation:

`y=(x+3)^2-12`