Solution
Hypotheses:
- The population mean is 132. In order to test the claim that the mean is 132, we should check for if the mean is not 132.
- Thus, the Hypotheses are:
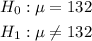
Test statistic:
- The test statistic has to be a t-statistic because the sample size (n) is less than 30.
- The formula for finding the t-statistic is:

- Applying the formula, we have:
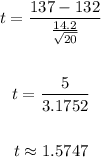
Critical value:
- The critical value t-critical, is gotten by reading off the t-distribution table.
- For this, we need the degrees of freedom (df) which is gotten by the formula:
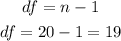
- And then we also use the significance level of 0.1 and the fact that it is a two-tailed test to trace out the t-critical. (Note: significance level of 0.1 implies 10% significance level)
- This is done below:
- The critical value is 1.729
P-value:
- To find the p-value, we simply check the table for where the t-statistic falls.
- The t-statistic given is 1.5747. We simply check which values this falls between in the t-distribution table. It falls between 1.328 and 1.729. We can simply choose a value between 0.1 and 0.05 and multiply the result by 2 since it is a two-tailed test.
- However, we can also use a t-distribution calculator, we have:
- Thus, the p-value is 0.13183
Final Conclusion:
- The p-value is 0.13183, and comparing this to the significance level of 0.1, we can see that 0.13183 is outside the rejection region.
- Thus, the result is not significant and we fail to reject the null hypothesis