When an object decelerates to a stop from an initial speed v with an acceleration a, the distance d traveled by the object is given by:
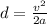
Then, the initial speed can be calculated as:
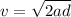
On the other hand, the acceleration of an object skidding through a horizontal surface with a coefficient of friction μ is:
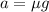
Where g=9.81m/s^2 is the gravitational acceleration.
Then, the initial speed is given in terms of known variables as:
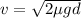
Replace the values to find the initial speed of the car:
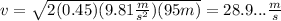
Therefore, the initial speed of the car was 28.9m/s.