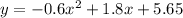Vertex form of a quadratic equation:
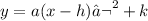
+a if the parabola opens up
-a if the parabola opens down
(h,k) coordinates of the vertex
For the given parabola:
It opens down
Vertex: (1.5, 7)

Use 1 point in the parabola in the equation above to find the value of a:
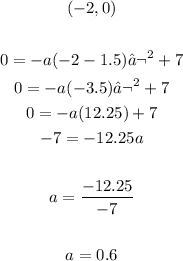
Then, the equation of the parabola in vertex form is:
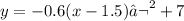
To write it in standard form:
1. Expand the expresion in parentheses:
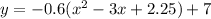
2. Remove the parentheses and simplify:
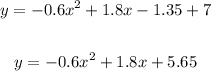
Then, the equation of the parabola in standard form is: