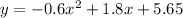Question

Find the standard and vertex formVertex (1.5 , 7 )

Answer 1

Vertex form of a quadratic equation:

`y=a(x-h)\placeholder{⬚}^2+k`

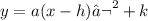
+a if the parabola opens up

-a if the parabola opens down

(h,k) coordinates of the vertex

For the given parabola:

It opens down

Vertex: (1.5, 7)

`y=-a(x-1.5)\placeholder{⬚}^2+7`

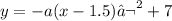
Use 1 point in the parabola in the equation above to find the value of a:

`\begin{gathered} (-2,0) \\ \\ 0=-a(-2-1.5)\placeholder{⬚}^2+7 \\ 0=-a(-3.5)\placeholder{⬚}^2+7 \\ 0=-a(12.25)+7 \\ -7=-12.25a \\ \\ a=(-12.25)/(-7) \\ \\ a=0.6 \end{gathered}`

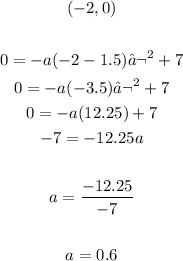
Then, the equation of the parabola in vertex form is:

`y=-0.6(x-1.5)\placeholder{⬚}^2+7`

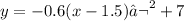
To write it in standard form:

1. Expand the expresion in parentheses:

`y=-0.6(x^2-3x+2.25)+7`

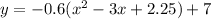
2. Remove the parentheses and simplify:

`\begin{gathered} y=-0.6x^2+1.8x-1.35+7 \\ \\ y=-0.6x^2+1.8x+5.65 \end{gathered}`

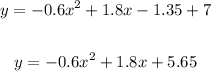
Then, the equation of the parabola in standard form is:

`y=-0.6x^(2)+1.8x+5.65`