Question

The safe loadLof a wooden beam supported at both ends varies jointly as the width, w, the square of the depth, d, and inversely as the lengthA wooden beam inwide7 indeep, and 13 ft long holds up 7172 What load would a beam 3 inwide, 3 indeep and 18 ft long of the same material support? (Round off your answer to the nearest pound)

Answer 1

Given:

The load varies as width and square of the depth and inversely as the length,

L₁=7127 lb

w₁=5 in=0.42 ft

d₁=7 in=0.58 ft

l₁=13 ft

w₂=3 in=0.25 ft

d₂=3 in=0.25 ft

l₂=18 ft

To find:

The load.

Step-by-step explanation:

From the question,

`L=(kwd^2)/(l)`

Where k is the proportionality constant.

Thus, substituting the 1st set of values in the above equation,

`\begin{gathered} L_1=(kw_1d_1^2)/(l_1) \\ 7172=(k*0.42*0.58)/(13) \\ \implies k=(7172*13)/(0.42*0.58) \\ =382742.2\text{ lb/ft}^2 \end{gathered}`

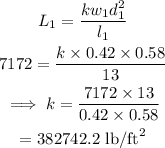
Substituting the second set of values,

`\begin{gathered} L=(382742.2*0.25*0.25)/(18) \\ =1329\text{ lb} \end{gathered}`

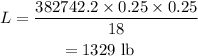
Final answer:

A 3 in wide, 3 in deep, and 18 ft long beam can support a load of 1329 lb