Given:
The load varies as width and square of the depth and inversely as the length,
L₁=7127 lb
w₁=5 in=0.42 ft
d₁=7 in=0.58 ft
l₁=13 ft
w₂=3 in=0.25 ft
d₂=3 in=0.25 ft
l₂=18 ft
To find:
The load.
Step-by-step explanation:
From the question,
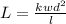
Where k is the proportionality constant.
Thus, substituting the 1st set of values in the above equation,
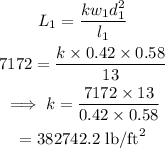
Substituting the second set of values,
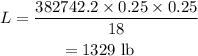
Final answer:
A 3 in wide, 3 in deep, and 18 ft long beam can support a load of 1329 lb