Recall that, according to the empirical rule:
1.- About 68% of the data falls within 1 standard deviation.
2.- About 99.7% of the data falls within 3 standard deviations.
Now, notice that:
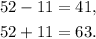
Therefore, approximately 68% of the students scored between 41, and 63.
Now, notice that:
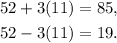
Therefore, approximately 99.7% of the students scored between 19 and 85.
Answer:
Approximately 68% of the students scored between 41, and 63.
Approximately 99.7% of the students scored between 19 and 85.