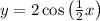Answer::
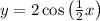
Explanation:
Given the general cosine function:
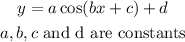
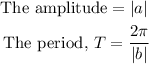
We want to determine the function that has the following properties:
• Amplitude = 2
,
• Period = 4π
Using the period formula given above:

From the given options, the function that satisfies the required property is: