From the given function :

The horizontal asymptotes depends on the coeficients of the highest degree between the numerator and the denominator.
Note that in any function :
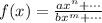
Where :
ax^n is the term with the highest degree in the numerator and
bx^m in the denominator.
If n < m :
The horizontal asymptote is y = 0
If n = m :
The horizontal asymptote is y = a/b
If n > m :
There is NO horizontal asymptote BUT there is a Slant Asymptote if n + 1 = m or n is exactly greater than m by 1.
Going back to the given function :
The term with the highest degree is 4x^5, so n = 5
For A. We need to find the values of N that will make the function have a horizontal asymptote of y = 0
From the note :
the values of n and m must be n < m
Since the value of n in the numerator is 5, the value of m in the denominator must be greater than 5
Assuming that the term -13x^N in the denominator has the highest degree.
N must be greater than 5
So N > 5
Now for B :
Values of N such that r(x) has a non-zero horizontal asymptote.
From the notes above, n must be equal to m (n = m).
Still, since the highest degree in the numerator is 5. The highest degree in the denominator must be equal to 5 also.
So N = 5
Then for C :
The horizontal asymptote from part B is y = a/b
a will be equal to 4
and
b will be equal to -13
So the asymptote in part B will be :

For D :
So to have a slant asymptote, n must be greater than m by 1.
Still, the highest degree in the numerator is 5.
So the degree of the denominator must be 4 to satisfy the condition (n + 1 = m)
Taking again the term -13x^N
N must be equal to 4
N = 4
For E :
Values of N such that r(x) has no HA and SA.
The rule is n > m
Still, from the numerator, n = 5
and m must be less than 5 except 4.
(Because if the value of m is 4, it will have a Slant asymptote like in Letter D)
So we can say that m must be less than 4
Therefore, from the denominator :
N < 4 or N = 0, 1, 2 and 3