Question

Consider the interval between x = -3 and x = 0. Explain whythe product of the linear factors results in g(x) being negativeand why the function changes from decreasing to increasing.

Answer 1

The graph of g(x) is a parabola, a parabola has the form:

`y=ax^2+bx+c`

Which is basically a quadratic function, if we multiply f(x) by x, the result is:

`\begin{gathered} g(x)=x\cdot f(x)=x\cdot(x+3) \\ Using_{\text{ }}distributive_{\text{ }}property\colon \\ g(x)=x^2+3x \end{gathered}`

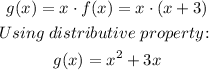
After we multiply the linear factors (Linear equations) we get a quadratic equation, which makes sense from the graph.

Now, the function g(x) changes from decreasing to increasing at the point (-1.5, -2.25) because that is the location of the vertex:

The vertex of the parabola is the maximum or minimum point on the graph of the quadratic function, it can be calculated as:

`\begin{gathered} V(h,k)\colon \\ h=-(b)/(2a) \\ where \\ b=3 \\ a=1 \\ h=-(3)/(2(1))=-(3)/(2)=-1.5 \\ k=g(h)=g(-1.5)=(-1.5)^2+3(-1.5)=-2.25 \\ so\colon \\ V(h,k)=(-1.5,-2.25) \end{gathered}`

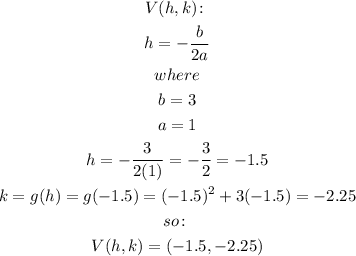
So, the function reaches its minimum point at the vertex, then it starts to increasing as x increases.