For the minimum value, the first derivative of function is equate to zero and value of second derivative is posiive.
Determine the first derivative of cost function.
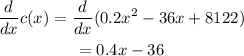
For maximum and minimu value,

Determie the second derivative of the cost function.
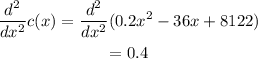
The second derivative of cost function is positive for all value of x. So x = 90 machines corresponds to the minimum value of function.
Answer: 90 machines