The point here is to calculate the area of the curve between 200 to 800 because it's a distribution of probability and even more, it's a normal distribution then look at it we can already see that the standard variation is 100 and the mean is 500, then
![\begin{gathered} X\sim N(500,100^2) \\ X\operatorname{\sim}N(\mu,\sigma^2) \end{gathered}]()
Then we must find
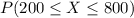
In fact, we are doing

The normal distribution is symmetrical then
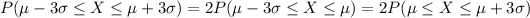
Therefore we can just evaluate
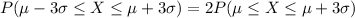
But why use the standard deviation and the mean? because we already know that value!
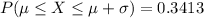
For 2*standard deviation

And our case, for 3*standard deviation
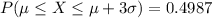
Therefore

Let's go back to our original equation
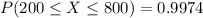
Then 99.74% of the students score between 200 and 800, now just do 99.8% of 1000
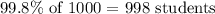
Hence, 998 students scored between 200 and 800