Question

Suppose we want to choose 2 colors, without replacement, from the 4 colors red, blue, green, and purple. How many ways can this be done, if the order of the choices is relevant? How many ways can this be done, if the order of the choices is not relevant?

Answer 1

We can solve this question as follows:

• We want to choose 2 colors ,without replacement, from 4 colors.

Then, we have:

1. If the order of the choices is relevant:

We can use the next formula:

`n=4,k=2\Rightarrow(n!)/((n-k)!)\Rightarrow(4!)/((4-2)!)=(4\cdot3\cdot2!)/(2!)=12`

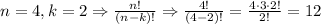
Therefore, we can choose 2 colors, without replacement, from the 4 colors, if the order of choices is relevant in 12 different ways.

2. If the order of the choices is not relevant:

We can use the next formula:

`n=4,k=2\Rightarrow(n!)/((n-k)!k!)=(4!)/((4-2)!2!)=(4\cdot3\cdot2!)/(2!\cdot2!)=(4\cdot3)/(2\cdot1)=(12)/(2)`

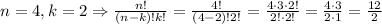
And finally:

`(12)/(2)=6`

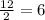
Therefore, we can choose 2 colors, without replacement, from the 4 colors, if the order of the choices is not relevant in 6 different ways.