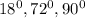Question

in a triangle the second angle measures four times the first. The measure of the third angle is 18⁰ more than the measure of the second. find the measure of the three angles

Answer 1

Let 'x' represent the measure of the first angle.

Let 'y' represent the measure of the second angle.

Let 'z' represent the measure of the third angle.

From the statement,

`\begin{gathered} y=4* x=4x \\ y=4x \end{gathered}`
`\begin{gathered} z=18^0+y=18^0+4x \\ z=18^0+4x \end{gathered}`

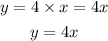
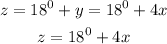
Note: The sum of angles in a triangle is 180°.

Therefore,

`x+4x+18^0+4x=180^0`

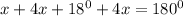
Solve for x

`\begin{gathered} x+4x+4x+18^0=180^0 \\ 9x+18^0=180^0 \\ 9x=180^0-18^0 \\ 9x=162^0 \end{gathered}`

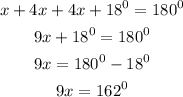
Divide both sides by 6

`\begin{gathered} (9x)/(9)=(162^0)/(9) \\ x=18^0^{} \\ \therefore x=18^0 \end{gathered}`

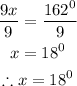
Substitute x = 27° into the measure of the second angle and solve for y

`\begin{gathered} y=4*18^0=72^0 \\ \therefore y=72^0^{} \end{gathered}`

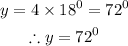
Let us now solve for z, which is the third angle

`\begin{gathered} z=18^0+72^0=90^0 \\ \therefore z=90^0 \end{gathered}`

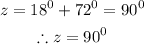
Hence, the measure of the three angles are

`18^0,72^0,90^0`