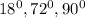Let 'x' represent the measure of the first angle.
Let 'y' represent the measure of the second angle.
Let 'z' represent the measure of the third angle.
From the statement,
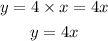
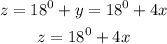
Note: The sum of angles in a triangle is 180°.
Therefore,

Solve for x
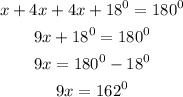
Divide both sides by 6
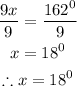
Substitute x = 27° into the measure of the second angle and solve for y

Let us now solve for z, which is the third angle

Hence, the measure of the three angles are