the exact value of cos(α - β) = 33/65
Step-by-step explanation:
tan α = -12/5
where angle α lies in the 2nd quadrant
In the second quadrant, only sine is positive. tan and cos will be negative
cos β = 3/5
where angle β lies in the 4th quadrant
In the 4th quadrant, only cos is positive. tan and sin will be negative
We are to find cos(α - β)
In trigonometry identity:
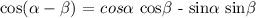
we need to find cosα, sinα and sin β
![\begin{gathered} \tan \text{ = opposite/adjacent} \\ \text{opp = 12, adj = 5},\text{ hyp} \\ \text{hyp}^2=(-12)^2+5^2\text{ = 169 } \\ \text{hyp = }\sqrt[]{169} \\ \text{hyp = 13} \\ \\ \cos \alpha\text{ = }(adj)/(hyp) \\ \cos \alpha\text{ = }(5)/(13) \\ Since\text{ }\cos \text{ is negative in II, }\cos \alpha\text{ = -}(5)/(13) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iqz5mws07gb1rtema3evz9j94fg5c6en2g.png)
Next we will find sinα:
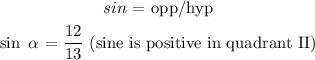
Next we wll find sin β:
![\begin{gathered} \sin \text{ = opp/hyp} \\ \cos \beta=(3)/(5) \\ \cos \text{ = adj/hyp} \\ \text{adj = 3, hyp = 5} \\ \text{hyp}^2=opp^2+adj^2 \\ 5^2\text{ = }opp^2+\text{ }3^2 \\ \text{opp}^2\text{ = 25 -9} \\ \text{opp = }\sqrt[]{16}\text{ = 4} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/56m4pwf6enmbvv33i41tp9jzyeqg4wc5kf.png)
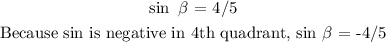
substitute the values:
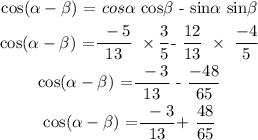
simplify:
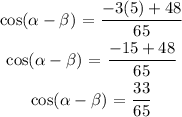
Hence, the exact value of cos(α - β) = 33/65