Answer:
63.7%
Step-by-step explanation:
To know the probability, we need to calculate the area of the circle and the area of the square.
The area of the circle is equal to:
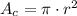
Where r is the radius of the circle and π is approximately 3.14. So, the area of the circle is:
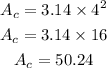
On the other hand, the area of the square is equal to:
![\begin{gathered} A_s=\text{Base}* Height \\ A_s=4\sqrt[]{2}*4\sqrt[]{2} \\ A_s=32 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nbkf5825s97yhn8zkmwwj4w4d5gl191tso.png)
Now, the probability that a randomly selected point within the circle falls in the square area is equal to the ratio of the areas calculated above. So, the probability is:
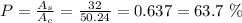
Therefore, the answer is 63.7%