Question

Determine if the lines are perpendicular y=2/3x+13y+2x=4

Answer 1

No, the lines are not perpendicular

Step-by-step explanation:

Two lines are perpendicular if the multiplication of their slopes is equal to -1.

Therefore, we first need to identify the slopes of each equation:

For y = (2/3)x+1, the slope is 2/3 because it is the number beside the x.

On the other hand, to know the slope of the equation 3y + 2x = 4, we need to solve for y, so:

`\begin{gathered} 3y+2x=4 \\ 3y+2x-2x=4-2x \\ 3y=-2x+4 \\ (3y)/(3)=(-2x)/(3)+(4)/(3) \\ y=-(2)/(3)x+(4)/(3) \end{gathered}`

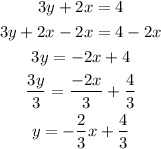
Therefore, the slope of the second equation is -2/3

Then, the multiplication of 2/3 by -2/3 is equal to:

`(2)/(3)*-(2)/(3)=(2*(-2))/(3*3)=-(4)/(9)`

Since -4/9 and -1 are distinct, the lines are not perpendicular.