Question

Graph a line that is parallel to the given line. Determine the slope of the given line and the one you graphed in the simplest form.

Answer 1

ANSWER and EXPLANATION

We want to graph a line that is parallel to the line graphed below.

Since they are both straight lines, the equation of the graph will be:

`y=mx+b`

A line that is parallel to another will have the same slope. This means that the slopes of both lines are equal.

Since we want to plot a random line that is parallel to the given line, the line can pass through any point.

Let the new graph pass through (1, 2).

Now, let us find the slope of the given line by using the formula:

`m=(y_2-y_1)/(x_2-x_1)`

This means that we have to pick two points that lie on the given line. Let us pick (-1, 0) and (0, -4). Therefore, the slope is:

`\begin{gathered} m=(-4-0)/(0-(-1))=(-4)/(0+1)=(-4)/(1) \\ m=-4 \end{gathered}`

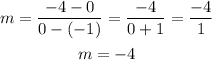
This is the same as the slope of the parallel line.

Now, to find the equation of the line, we have to apply the point-slope method using the point (1, 2) and slope of -4:

`y-y_1=m(x-x_1)_{}`

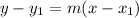
Therefore, we have:

`\begin{gathered} y-2=-4(x-1) \\ y-2=-4x+4 \\ y=-4x+4+2 \\ y=-4x+6 \end{gathered}`

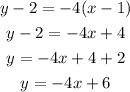
That is the equation of the line. Now, we can find another point in order to graph the line.

Let x = 0, therefore, we have:

`\begin{gathered} y=0+6 \\ y=6 \end{gathered}`

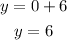
Hence, we have two points (0, 6) and (1, 2)

Let us plot the graph now:

The red line represents the new graph.