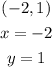Question

solve the following system of equations graphically on the set of axes below. y= -2x -3 y= ½ x +2 (please draw it out & give me the solution)

Answer 1

The solution to the system of equation is the point which the two lines meet.

`\begin{gathered} (-2,1) \\ x=-2 \\ y=1 \end{gathered}`

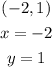
Step-by-step explanation:

Given the system of equation;

`\begin{gathered} y=-2x-3 \\ y=(1)/(2)x+2 \end{gathered}`

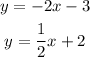
To plot the linear graphs, le us derive two ordered pairs on each equation;

`\begin{gathered} At\text{ x = 2} \\ y=-2x-3=-2(2)-3 \\ y=-7 \\ (2,-7) \\ \\ y=(1)/(2)x+2 \\ y=(1)/(2)(2)+2 \\ y=1+2 \\ y=3 \\ (2,3) \end{gathered}`
`\begin{gathered} at\text{ x = -2} \\ y=-2x-3=-2(-2)-3 \\ y=4-3 \\ y=1 \\ (-2,1) \\ \\ y=(1)/(2)x+2 \\ y=(1)/(2)(-2)+2 \\ y=-1+2 \\ y=1 \\ (-2,1) \end{gathered}`

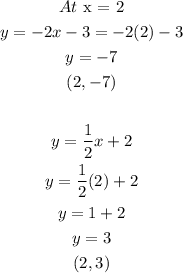
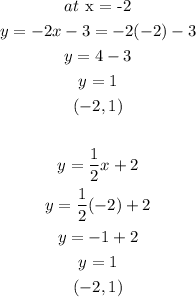
Graphing the points we have;

Therefore, the solution to the system of equation is the point which the two lines meet.

`\begin{gathered} (-2,1) \\ x=-2 \\ y=1 \end{gathered}`