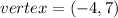Question

Complete the square to find the minimum value of the expression 4x^2 + 8x + 23 Minimum=???

Answer 1

We are given the following quadratic equation

`4x^2+8x+23`

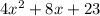
Let us apply the completing the square method to the given equation.

Take the square of the half of the middle term coefficient (that is 8)

`((8)/(2))^2=(4)^2=16`

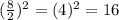
Add and subtract this value from the given equation

`4x^2+8x+23+16-16`

Re-write the equation as below

`(4x^2+8x+16)+23-16`

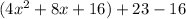
The terms in the parenthesis will be a perfect square so we can factor it out as

`\begin{gathered} (4x^2+8x+16)+23-16 \\ \mleft(x+4\mright)^2+23-16 \\ \mleft(x+4\mright)^2+7 \end{gathered}`

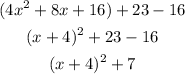
Finally, compare this equation with the vertex form given by

`(x-h)^2+k`

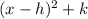
So, we have

h = -4

k = 7

The vertex (h, k) = (-4, 7) is the minimum point of the given quadratic equation

`vertex=(-4,7)`