We are given that from a standard deck 2 cards are drawn without replacement. In a standard deck, there are 26 red cards and 26 black cards for a total of 52 cards. There are 13 hearts, 13 diamonds, 13 clubs, and 13 spades. Therefore, the probability of drawing a heart is:
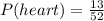
Since there is already one card drawn this means that there are now 51 cards, also since hearts are also red cards this means that there are now 25 red cards. Therefore, the probability of getting a red card is:
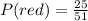
Now, to determine the probability of getting both a hear and a red card is determined using the product rule for probabilities:
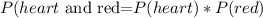
Substituting the values:
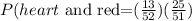
Solving the operations:
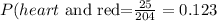
Therefore, the probability is 0.123