Question

find the average velocity if the take-off velocity of an airplane on a run away is 300 km/hr with an acceleration of 1 m/s^2

Answer 1

Given:

The takeoff velocity of the plane, v=300 km/hr

The acceleration of the plane, a=1 m/s²

To find:

The average velocity of the plane.

Step-by-step explanation:

The initial velocity of the plane is u=0 m/s

The take-off velocity of the plane in m/s is

`\begin{gathered} v=300*(1000)/(3600) \\ =83.33\text{ m/s} \end{gathered}`

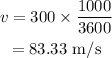
The average velocity of an object having a constant acceleration is given by the sum of the initial and final velocity divided by two.

Thus the average velocity of the plane until it takes off is given by,

`\begin{gathered} v_(av)=(u+v)/(2) \\ =(0+83.33)/(2) \\ =41.7\text{ m/s} \end{gathered}`

From the equation of motion,

`v^2-u^2=2ad`

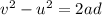
Where d is the takeoff distance.

On substituting the known values,

`\begin{gathered} 83.33^2-0=2*1* d \\ \Rightarrow d=(83.33^2)/(2*1) \\ =3471.9\text{ m} \end{gathered}`

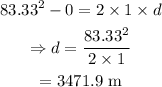
Final answer:

Thus the average velocity of the plane is 41.7 m/s

Thus the takeoff distance is 3471.9 m