Question

A) what is the probability that a student who has chores also has a curfew? B) what is the probability that a student who has a curfew also has chores? C) Are the two events have chores and have a curfew independent? Explain.

Answer 1

A. The probability that a student who has chores also has a curfew.

The total number of students that have chores is 75.

Out of these 75, 51 also have a curfew.

So, the probability that a student who has chores also has a curfew is;

`(51)/(75)`

B. The probability that a student who has a curfew also has chores.

The total number of students that have a curfew is 81.

Out of these 75, 51 also have chores.

So, the probability that a student who has a curfew also has chores is;

`(51)/(81)`

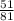
C. To check for independence between the 2 events (chores and curfew), we perform a p-test of independence.

The square is a 2 x 2 square, therefore, the degree of freedom is (2-1)(2-1)=1

The chi-square value is;

`\chi^2=0.149`

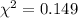
We obtain the p-value as;

`p=0.6999`

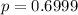
Since p > 0.05, the events chores and curfew are independent.