Question

Two buses leave Nashville at the same time traveling in opposite directions. One bus travels at 58 mph and the other at 61 mph. How soon will they be 416.5 milesapart?

Answer 1

These types of problems can be easily solved using the concept of relative speed.

Consider that the relative speed of one body with respect to another, while moving in opposite directions is equal to the sum of the magnitude of the speeds of both the bodies.

Given that the buses move with speeds of 58 mph and 61 mph in opposite directions. So their relative speed (v) with respect to each other will be,

`\begin{gathered} v=58+61 \\ v=119 \end{gathered}`

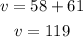
Now, consider that the distance travelled, speed, and time taken, are related as,

`\begin{gathered} \text{Time}=\frac{Distance}{\text{Speed}} \\ t=(d)/(v) \end{gathered}`

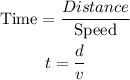
So the time required by the buses to be 416.5 miles apart is calculated as,

`\begin{gathered} t=(416.5)/(119) \\ t=3.5 \end{gathered}`

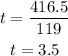
Thus, the buses will be 416.5 miles apart after 3.5 hours.