Given:
Equation of a circle is
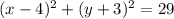
Required:
What is the center and the radius of the circle?
Step-by-step explanation:
In a circle, if the coordinate of the center are (h, k), r is the radius, and (x, y) is any point on the circle., then the center of circle formula is given by

Now, we have equation
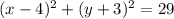

Answer:
Hence, above is the center and radius of circle.