We have the following equation:
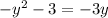
by moving -3y to the left hand side, we have
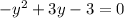
which is in the form
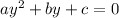
By comparing both equations, we can see that a=-1, b=3 and c=-3. By substituting these values in the quadratic formula, we get
![y=\frac{-3\pm\sqrt[]{3^2-4(-1)(-3)}}{2(-1)}](https://img.qammunity.org/2023/formulas/mathematics/college/i3v4yt48wn54iod9zllx05msoduqlb65x8.png)
which gives
![y=\frac{-3\pm\sqrt[]{9-12}}{-2}](https://img.qammunity.org/2023/formulas/mathematics/college/6xj30xxnt45ij38mh24gznttugmrbgde2j.png)
which leads to
![y=\frac{-3\pm\sqrt[]{-3}}{-2}](https://img.qammunity.org/2023/formulas/mathematics/college/2acnqtdaotaqx0xssrdzx7ezcp81v9utcm.png)
but
![\begin{gathered} \sqrt[]{-3}=√(3)i \\ \text{where} \\ i=\sqrt[]{-1},\text{ the imaginary number} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/grrfjhj5lr2tx7y0er96q2mgxko0shdx90.png)
Therefore, the solutions are:
![\begin{gathered} y_1=\frac{-3+\sqrt[]{3i}}{-2} \\ \text{and} \\ y_2=\frac{-3-\sqrt[]{3}i}{-2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/e9dto5dqtlb5fx9jtz8m2mq1lzs3brtqxf.png)