Question

Quadratic Equations:Solve the following quadratic equation using the quadratic formula: formula attached, picture -y^2 - 3 = -3y

Answer 1

We have the following equation:

`-y^2-3=-3y`

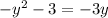
by moving -3y to the left hand side, we have

`-y^2+3y-3=0`

which is in the form

`ay^2+by+c=0`

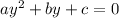
By comparing both equations, we can see that a=-1, b=3 and c=-3. By substituting these values in the quadratic formula, we get

`y=\frac{-3\pm\sqrt[]{3^2-4(-1)(-3)}}{2(-1)}`

which gives

`y=\frac{-3\pm\sqrt[]{9-12}}{-2}`

which leads to

`y=\frac{-3\pm\sqrt[]{-3}}{-2}`

but

`\begin{gathered} \sqrt[]{-3}=√(3)i \\ \text{where} \\ i=\sqrt[]{-1},\text{ the imaginary number} \end{gathered}`

Therefore, the solutions are:

`\begin{gathered} y_1=\frac{-3+\sqrt[]{3i}}{-2} \\ \text{and} \\ y_2=\frac{-3-\sqrt[]{3}i}{-2} \end{gathered}`