In the given figure,
Circles are drawn considering the sides AB and AC as diameters.
The circle intersects at point D.
Point D lies on side BC.
Draw a perpendicular from point A on BC intersecting at D.
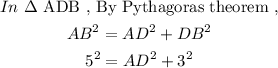
Further,
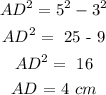
Further,
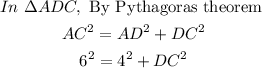
Therefore,
![\begin{gathered} DC^2=6^2-4^2 \\ DC^2=\text{ 36 - 16} \\ DC^2=\text{ 20} \\ DC\text{ = 2}\sqrt[]{5}cm \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ykrdxjrglctbs53zdusdvzuqt960kiiqem.png)
The value of BC is calculated as,
![\begin{gathered} BC\text{ = BD + DC} \\ BC\text{ = 3 + 2}\sqrt[]{5} \\ BC\text{ = }(\text{ 3 + 2}\sqrt[]{5}\text{ ) }cm \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/876vdfhphlnfaadrf9dqf70tbd2s3nii1h.png)
Thus the value of BC is ,
![(\text{ 3 + 2}\sqrt[]{5}\text{ ) }cm](https://img.qammunity.org/2023/formulas/mathematics/college/eeexosr7g6jsvcbgajd01xrbadsx9htj8k.png)