You are asked to perform:
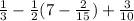
Wee need to start with the parenthesis.
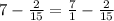
We the numerator will be 7 times 15 minus 2 (2x1), and the denominator will be 15 (15x1)

Now, the expression to solve is:

We need to perform the multiplication first (the second term)

Now, the expression to solve will be:
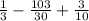
Now we can solve either the substraction or the sum. Let's go first with the substraction:
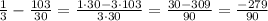

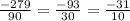
Note that it could be simplified twice, dividing both numerator and denominator by 3.
Then, the expression to solve is reduced to:
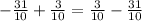
We can make that substraction easily since they have the same denominator. 3 - 31 = -28
Then, the first expressions equals to:
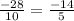
Then, the full answer will be:
