Question

Mike solved a system of equations and found that it had infinite solutions. Which could be the system of equations mike solved?

Answer 1

A system of equations has infinite solutions when both equations are equivalent.

To check if two equations are equivalent, write both of them in the same form. If the coefficients are proportional, including the constant terms, then they are equivalent.

Option 1

The first equation is written in general form. Isolate the constant term on the second equation to write it in general form:

`\begin{gathered} y=-2x-1 \\ \Rightarrow2x+y=-1 \end{gathered}`

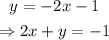
Notice that if we multiply the second equation by 3 on both sides, we will get the same coefficients as in equation 1:

`\begin{gathered} 3(2x+y)=3(-1) \\ \Rightarrow6x+3y=-3 \end{gathered}`

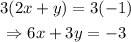
Then, both equations are equivalent.

Therefore, this system has infinite solutions.

Option 2

Since there is no constant term in the secon