Remember that
The formula to calculate continuously compounded interest is equal to
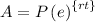
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is the Number of Time Periods
e is the mathematical constant number
In this problem, we have that
Part 1
P=$13,000
A=$26,000
t=14 years
substitute given values

Part 2
we have
P=$13,000
r=5%=0.05
t=26 years
substitute in the formula
![\begin{gathered} A=13,000(e)^{\operatorname{\{}0.05*26\operatorname{\}}} \\ A=\$47,700.86 \end{gathered}]()