Question

Mark biked to the park on Saturday. It tookhim 10 minutes to get there. While he wasthere, his bike broke and he had to walkhome. It took him 25 minutes to walk home.He can bike 6 mph faster than he can walk.How fast can he bike?

Answer 1

Let the distance from his home to the park be d .

The time it took him to bike home in hours is given by

`(10)/(60)=(1)/(6)\text{hours}`

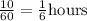
The time it took him to walk home in hours is given by

`(25)/(60)=(5)/(12)\text{ hours}`

`\text{speed }=(dis\tan ce)/(time)`

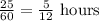
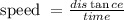
Hence, the speed with which he biked home is given by

`d/(1)/(6)=d*6=6d\text{ mph}`

The speed with which he walk home is given by

`d/(5)/(12)=d*(12)/(5)=\frac{12d\text{ }}{5}\text{mph}`

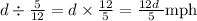
Since, he can bike 6 mph faster than he can walk, then

`6d=(12d)/(5)+6`

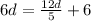
Subtracting 12d/5 from both sides we have

`\begin{gathered} 6d-(12d)/(5)=6 \\ (18d)/(5)=6 \end{gathered}`

Multiplying both sides by 5/18 we have

`\begin{gathered} (18d)/(5)*(5)/(18)=(6)/(1)*(5)/(18) \\ d=(5)/(3)=1(2)/(3) \end{gathered}`

Therefore,

`6d=(6)/(1)*(5)/(3)=2*5=10`

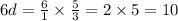
Hence, the speed of the bike is 10 mph