We are given the next polynomial, and are asked to factor it:

We are going to use the perfect square formula, which states that:

Therefore, we need to rewrite our polynomial. We start by factoring the number 25 and applying the exponent rule, as follows:
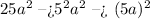
Now, we factor the second term, as follows:
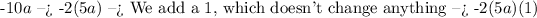
Finally, we rewrite our last term as:
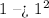
With these, we have that our initial polynomial is:
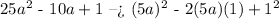
And we see that we already have it in the form that we need to apply the perfect square formula, in which 5a is b and 1 is c, so we apply it just as follows:
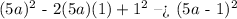
And therefore, (5a - 1)² is the answer