Question

In 1990, there were 112 nuclear power plants in the U.S. By 2019, this number had fallen to 96.(a) Write a linear model to describe the number of nuclear power plants from 1990 onward.Pt = (b) Using this linear model, predict the number of nuclear power plants in the U.S. in 2031. Round your answer to the nearest whole number. nuclear plants(c) When do you expect the number of nuclear plants to reach 75? Give your answer as a calendar year (ex: 2020).During the year

Answer 1

(a) We want a linear model to describe the number of nuclear power plants from 1990 onward.

Let "x" be the year and "y" be the number of nuclear power plants.

We are given two points: (1990, 112) and (2019, 96).

If we have two points, we can find a line that passes through them. To do this, we first can find the slope.

The slope can be found by dividing a difference in a y-values by a difference in the x-values:

`s=(y_2-y_1)/(x_2-x_1)`

Where, the suibscripts represent the points. Inputting our given points, we have:

`\begin{gathered} x_1=1990 \\ y_1=112 \\ x_2=2019 \\ y_2=96_{} \\ s=(96-112)/(2019-1990)=-(16)/(29) \end{gathered}`

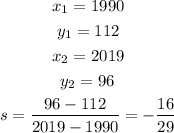
Now, we can use the slope-intercept form of line equation fo get the complete equation.

`\begin{gathered} y-y_1=s(x-x_1) \\ y-112=-(16)/(29)(x-1990) \\ y=-(16)/(29)x+(16)/(29)1990+112 \\ y=-0.5517x+1209.931 \end{gathered}`

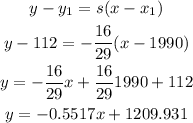
(b) To predict using this model, we just need to input this value into the equation. 2031 is the year, so it is a x-value, so x = 2031:

`y=-0.5517\cdot2031+1209.931=89.4283\approx89`

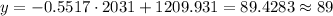
(c) The number of nuclear plants is the y-value, so we want y = 75:

`\begin{gathered} 75=-0.5517x+1209.931 \\ 75-1209.931=-0.5517x \\ -0.5517x=-1134.931 \\ x=(-1134.931)/(-0.5517)=2057.1524\ldots\approx2057 \end{gathered}`

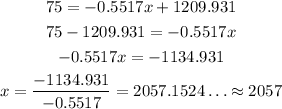
Given this model, it is expected that the number of nuclear plants reaches 75 by 2057.