Question

What’s the 5th term is 2,14,98

Answer 1

• 5th term = 50

Explanation:

In the question we have given an Arithmetic Progression ( A.P ) i.e. ,

• 2 , 14 , ....98

• What is Arithmetic Progression ?

→ An Arithmetic Progression is a list of numbers in which each term is obtained by adding a fixed number to the preceding term except the first term .

This fixed number is called the common difference of the A.P. and it can be positive, negative, or zero .For finding common difference we have to subtract first term from second term .

Formula :

`\longmapsto \: \blue{ \boxed{ a_ n = a + (n - 1)d }}`

Here ,

• an = nth term

• a = first term

• d = common difference

We know that ,

• a1 = 2

• a2 = 14

• last term ( l ) = 98

So , common difference of given a.p. :

• a2 - a1

• 14 - 2

• 12

Therefore , 12 is common difference of given a.p.

Now , substituting values in formula :

`\longmapsto \: a_(5) = 2 + (5- 1)12`

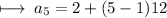
Step 1 : Solving parenthesis :

`\longmapsto \: a_5 = 2 +( 4) * 12`

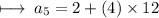
Step 2 : Multiplying 4 and 12 :

`\longmapsto \: a_5 = 2 + 48`

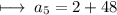
Step 3 : Adding 2 and 48 :

`\longmapsto \: \green{ \boxed{{{\bold{a_5 = 50}}}}}`

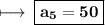
• Therefore , 5th term of the given a.p. is 50 .

#Keep Learning

Answer 2

`\bold{\huge{\orange{\underline{ Solution }}}}`

Correct Question :-

What is the 5th term of an AP 2 , 14 ....98 .

Given :-

We have AP,

• 
  `\sf{ 2 , 14 ,.... 98 }`
• AP is the arithmetic progression or a sequence of numbers in which succeeding number is differ from preceeding number by a common value.

Solution :-

We have an AP :- 2 , 14 .....98

Therefore,

• 
  `\sf{a1\: or \:1st\: term = 2 }`
• 
  `\sf{a2 \:or \:2nd\: term = 14 }`
• 
  `\sf{an \:or\: last\: term = 98}`

Here,

Common difference of an AP

`\sf{ a2 - a1 }`

`\sf{ = 14 - 2}`

`\sf{ = 12}`

Thus, The common difference is 12

Now,

We know that,

`\sf{an = a1 + ( n - 1 )d}`

`\sf{a5 = 2 + ( 5 - 1 )12}`

`\sf{a5 = 2 + 4 × 12}`

`\sf{a5 = 2 + 48}`

`\sf{\red{a5 = 50}}`

Hence, The 5th term of given AP is 50