Question

I need help with #3 of this problem. Thank you. The answer to #2 is d = log(I^20)

Answer 1

0.00018

Step-by-step explanation

First, we have to solve the equation from question 2 for I,

`d=\log (I^(20))`

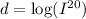
Raise 10 to each of the sides of the equation,

`\begin{gathered} 10^d=10^{\log (I^(20))} \\ 10^d=I^(20) \end{gathered}`

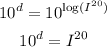
And take the 20th root to both sides,

`I=10^(d/20)`

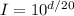
Now, we have to find the ratio of the intensity for the whisper and the intensity for the concert,

`(I_(whisper))/(I_(concert))=(10^(45/20))/(10^(120/20))=10^((45-120)/20)=10^(-3.75)\approx0.00018`

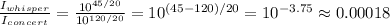
The intensity of a whisper is 0.00018 times the intensity of a rock concert.