ANSWER
0.00018
Step-by-step explanation
First, we have to solve the equation from question 2 for I,
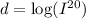
Raise 10 to each of the sides of the equation,
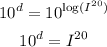
And take the 20th root to both sides,
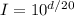
Now, we have to find the ratio of the intensity for the whisper and the intensity for the concert,
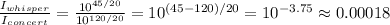
The intensity of a whisper is 0.00018 times the intensity of a rock concert.